Trees
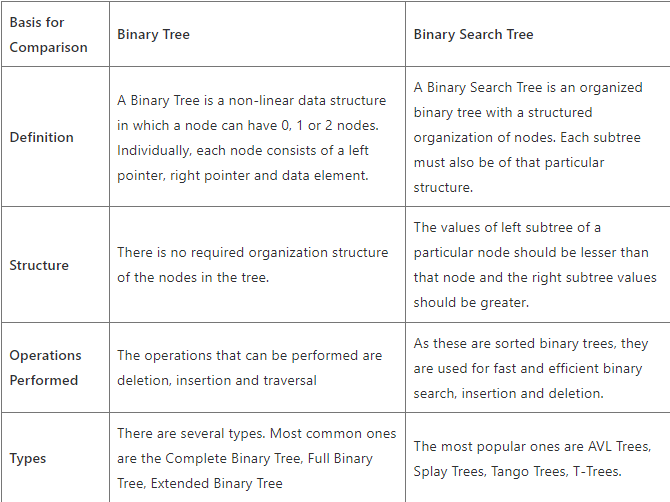
Common Terminology
- Root - The root is the node at the beginning of the tree
- K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
- Left - A reference to one child node, in a binary tree
- Right - A reference to the other child node, in a binary tree
- Edge - The edge in a tree is the link between a parent and child node
- Leaf - A leaf is a node that does not have any children
- Height - The height of a tree is the number of edges from the root to the furthest leaf
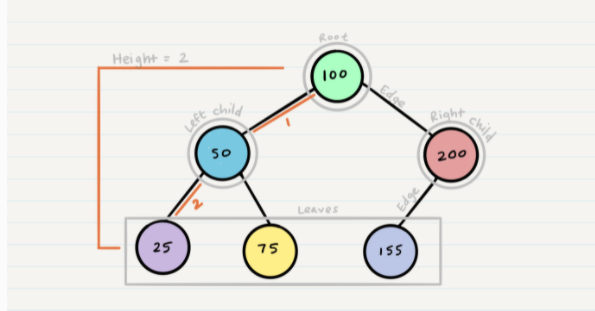
Traversals
1.Depth First
- Pre-order: root » left » right
- In-order: left » root » right
- Post-order: left » right » root
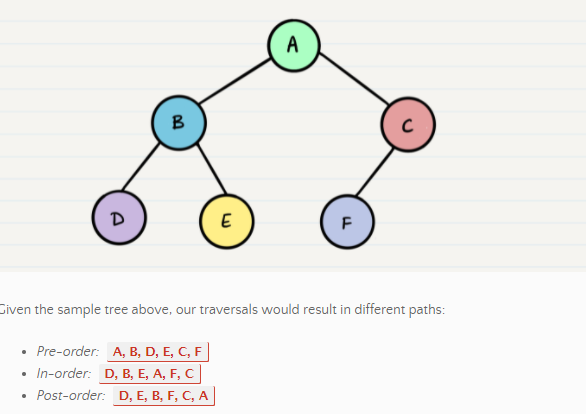
- The most common way to traverse through a tree is to use recursion.
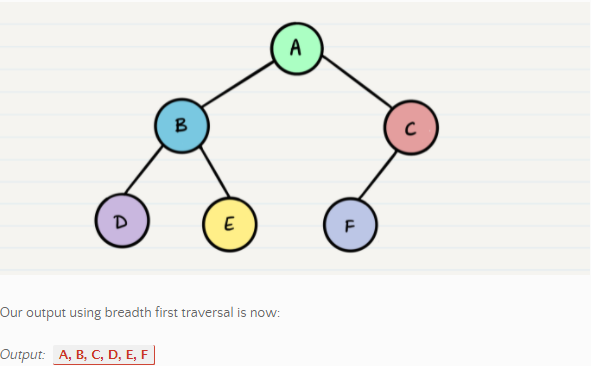
2.Breadth First
We go Level by level.
Big O
- The Big O time complexity for inserting a new node is O(n).
-
Searching for a specific node will also be O(n), worst case we will have to look at n items, hence the O(n) complexity.
- The Big O space complexity for a node insertion using breadth first insertion will be O(w), where w is the largest width of the tree.
- A perfect binary tree is one where every non-leaf node has exactly two children.
The maximum width for a perfect binary tree, is 2^(h-1), where h is the height of the tree. Height can be calculated as log n, where n is the number of nodes.
Binary Search Trees (BST)
- In a BST, nodes are organized in a manner where all values that are smaller than the root are placed to the left, and all values that are larger than the root are placed to the right.
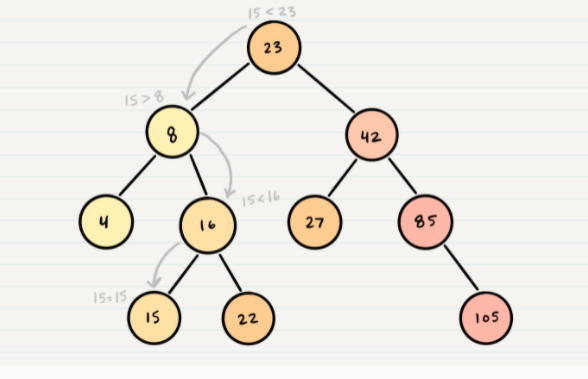
- The best way to approach a BST search is with a while loop. ‘ We cycle through the while loop until we hit a leaf, or until we reach a match with what we’re searching for.’
Big O
-
The Big O time complexity of a Binary Search Tree’s insertion and search operations is O(h), or O(height). (In the worst case, we will have to search all the way down to a leaf).
-
In a balanced (or “perfect”) tree, the height of the tree is log(n). In an unbalanced tree, the worst case height of the tree is n.
-
The Big O space complexity of a BST search would be O(1).
Binary Tree vs Binary Search Tree